Calculation of torque value of 'XM430-W350-T'

Support
, ,
1

Issue:

I want to know the exact torque value of the ‘XM430-W350-T’. To calculate the torque value, I found the torque-current graph at the following link, but I can’t determine the exact value because it’s only depicted as an image. If anyone knows how to calculate it accurately or has the data, I would appreciate it if you could let me know.

graph link :

‘XM430-W350-T’ E-mannual:

2

The torque and current are approximately proportional to one another, meaning that the simplest way to calculate the torque output for a given current would be:

Present Torque = Maximum Torque x (Present Current/Maximum Current)

3

Thank you for your response.
May I ask one more question?
When checking the ‘goal current’ of ‘XM450-W350-T’ in ‘Dynamixel Wizard,’ it can be adjusted from -1193 to 1193. In other words, the current can be adjusted from -3.20917A to 3.20917A. However, if you look at the performance graph above, it is no longer drawn beyond approximately 1.8A. Does this mean that the torque does not increase and remains constant at the torque value corresponding to 1.8A?

4

At that time if you look at the RPM graph its value is around 5 rpm so the motor is about to stall.

5

@cbnu167

This is a more detailed procedure using simultaneous equations (it is less rigorous than statistical regression), nonetheless it will do the job for you.

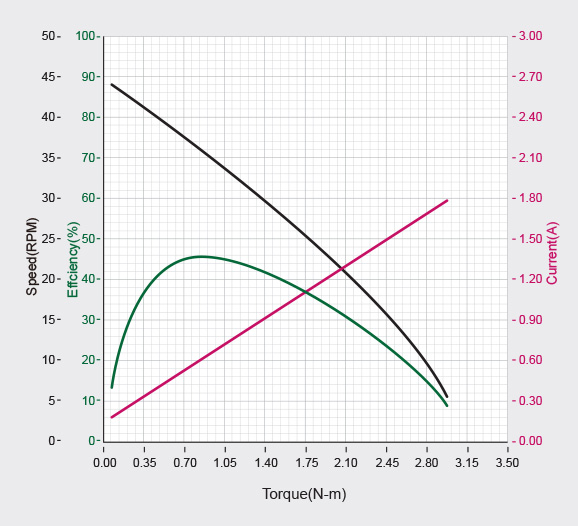
Fitting XM430-W350 Torque (T) vs Current (C) to a Linear Function from Performance Graph at (XM430-W350-T/R).

image

As the T vs C graph looks “linear”, we’ll try to fit a Linear Function to it, so:

T = a * C + b Eq. (1) - where Unknown Parameters are a and b

The “curve-fitting” procedure is listed below:

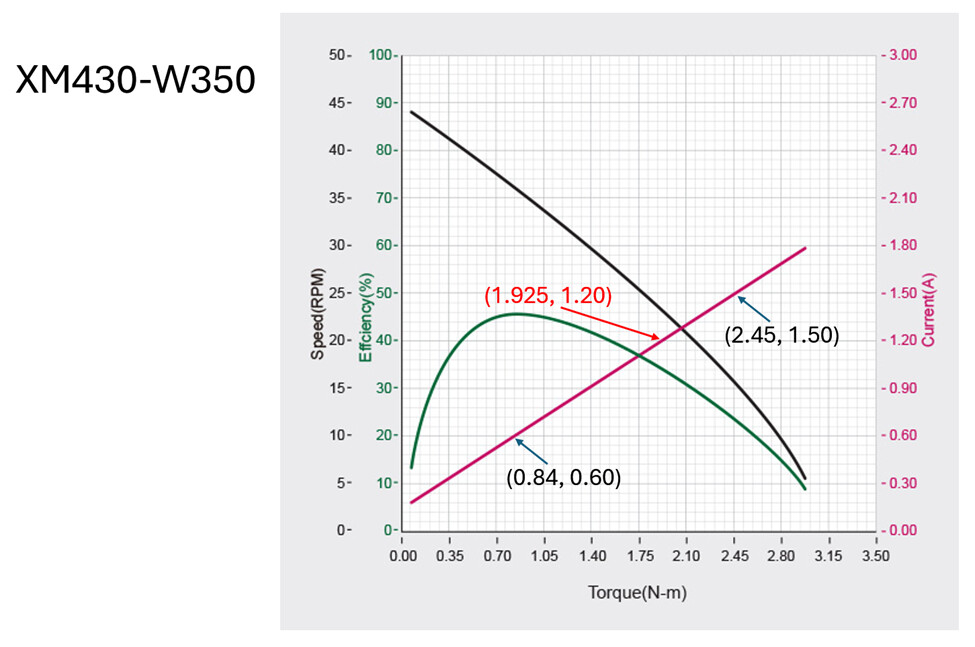
  • Find (T,C) coordinates for 3 points that are on the T/C Graph. I chose (0.84, 0.60), (2.45, 1.50) and (1.925, 1.20). We’ll use the 3rd data point (1.925, 1.20) to check our function fitting results.

  • To get rid of Parameter b, apply the first two Data Points to Eq. (1):

    • Using (0.84, 0.60), Eq. (1)] yields 0.84 = a * 0.60 + b Eq. (2)
    • Using (2.45, 1.50), Eq. (1)] yields 2.45 = a * 1.50 + b Eq. (3)

  • Determination of Parameter a:

    • [Eq. (2) – Eq. (1)] yields 1.61 = a *0.91 therefore a = 1.769

  • Determination of Parameter b with Eq. (2):

    • Eq. (2) is solved for b = 0.84 – (1.769 * 0.60) = -0.2214, so b = -0.2214

  • So, the T/C Performance Graph can be analytically represented as Eq. (4):

    T = 1.769 * C – 0.2214

    • Where C is in Amperes (A) and T is in Newton-Meter (N-m)

  • Checking the results with 3rd Data Point (1.925, 1.2):

    • Using C=1.2 in Eq. (4) yields T = 1.769 * 1.2 – 0.2214 = 1.9 (pretty close to 1.925 as shown on the graph).

Application in C++/Python programming

According to the XM430-W350 Control Table, at run-time, you can use DXL SDK to read in Present Current (PC126) at Address 126

(XM430-W350-T/R).

This PC126 number is supposed to be a signed 16-bit integer between (- Goal_Current) and (+Goal_Current), to be found at Address 102. By default, this range is between (-1193) and (+1193) – in decimal, and its unit value is 2.69 mA.

In ROBOTIS software/firmware, negative integers use the 2-complement binary format for a 16-bit integer, however Python/C++ does not know that in advance, so it would just print out the 2-complement integer as is (between 0 and 65535) – to the confusion of many users.

So, as a programmer for your Python/C++ code, you need to do some checking before converting PC126 into a C value that you can use with your Eq. 4 from above:

// Assuming 16-bit 2-complement integers - pseudo code

if (PC126 > 32767) // when NEGATIVE VALUES for PC126
PC126 = (65536 – PC126) * (-1); // this is a signed decimal integer

else // when POSITIVE VALUES for PC126
PC126 = PC126;

// Computing C in A, using abs(PC126)

C = abs(PC126) * 2.69 / 1000.0; // in A

T = 1.769 * C – 0.2214; // in N-m